Une réserve à soufflet mise en chiffres
Après différents avatars, je suis enfin parvenu à calculer les performances prévisibles des réserves à soufflet, à partir des caractéristiques de construction, ceci pour des réserves en pression ou en dépression.
En connaissant :
1 les dimensions des volets – longueur / largeur et leur débattement prévu,
2 les dimensions des éclisses,
3 Les caractéristiques du ressort, et le point d'application de la force de celui-ci,
vous pourrez calculer la pression prévisible que votre nouvelle réserve fournira, en fonction du déplacement du volet.
Je tiens à votre disposition une feuille de calcul Excel, ou bien je vous fais le calcul sur demande, en ayant les éléments ci-dessus.
Cela permet de faire, avant de bricoler et d'investir du temps et de l'argent, des essais virtuels de dimensions, de force de ressort, etc.
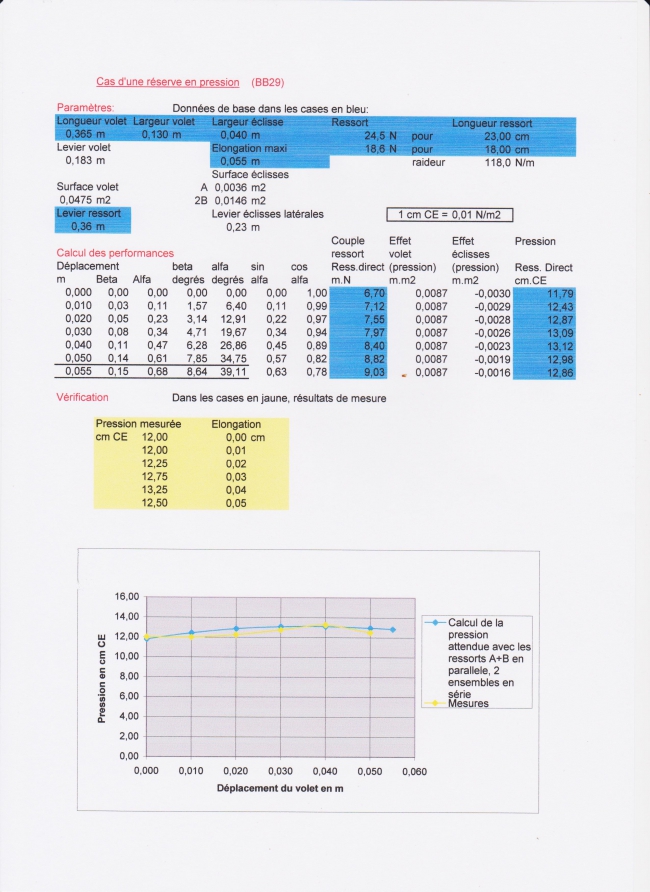
Par exemple, résultats pour mon OdB BB29
Justificatifs des calculs concernant une réserve à soufflet
Dimensions du volet mobile et ouverture
Ce que l’on veut L(ongueur) x l(argeur) d(débattement)
Ex : (ce que j’ai réalisé sur mon BB29) 36,5 cm x 13,0 cm - 6 cm
Dimensions des éclisses
(Voir annexe)
Surface des éclisses
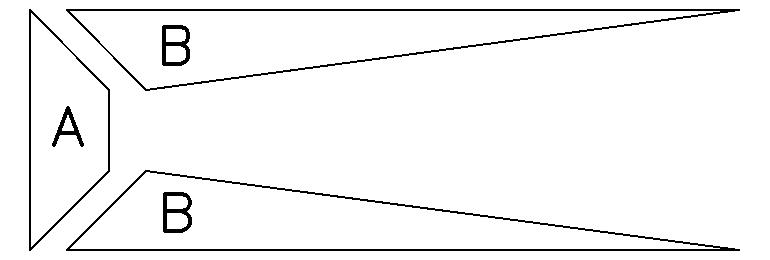
Surface A : Largeur volet x largeur éclisse - largeur éclisse (carré)
Surface B : Longueur volet x largeur éclisse (divisé par 2, multiplié par 2 éclisses)
Ex : A = 13 x 4,0 – 4,0 x 4,0 = 36 cm2
B = 36,5 x 4,0 = 146 cm2
Forces s’appliquant aux différents éléments – Couples correspondants.
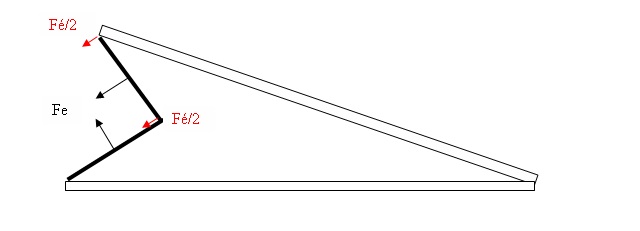
Le volet et les éclisses sous l’effet de la pression interne supportent chacun une force dont la valeur est de :
Force = pression exercée x surface concernée
et dont le point d’application est au centre de leur surface et qui est perpendiculaire à celle-ci.
Le couple résultant est le produit de la force par la distance de son point d'application au point d'articulation.
Pour le volet mobile :
Pour un volet donné et une pression effectivement constante, la force est constante et le couple résultant est constant.
Ex : 13 (cm d'eau) x 36,5 x 13 (= surface du volet en cm2) x 36,5 / 2 (distance point d'application – articulation en cm) soit avec les corrections d'unités 11,26 N.m
Pour les éclisses :
Les éclisses sont montées de telle façon que les forces sont convergentes et tendent à refermer l’angle que les éclisses forment entre elles. (NB : la situation serait différente si les éclisses étaient montées vers l’extérieur du soufflet.)
Sur une éclisse, si elle était rectangulaire, on pourrait décomposer cette force en deux forces égales, s’appliquant à chaque extrémité de la surface. Mais il convient de tenir compte des formes des éclisses, en trapèze ou en triangle, qui vont introduire un coefficient dans la façon dont ces forces sont réparties : (Voir annexe)
Pour A, en trapèze : une force Fé x 0,586 qui s’applique à l’articulation avec le volet mobile (ou avec le support) (grand côté), et Fé x 0,414 qui s’applique à l’articulation avec l’autre éclisse (petit côté) (toutes deux représentées en rouge).
Pour B, en triangle : une force Fé x 2/3 (0,66) qui s’applique à l’articulation avec le volet mobile (ou avec le support), et Fé x 1/3 (0,33) qui s’applique à l’articulation avec l’autre éclisse (toutes deux représentées en rouge).
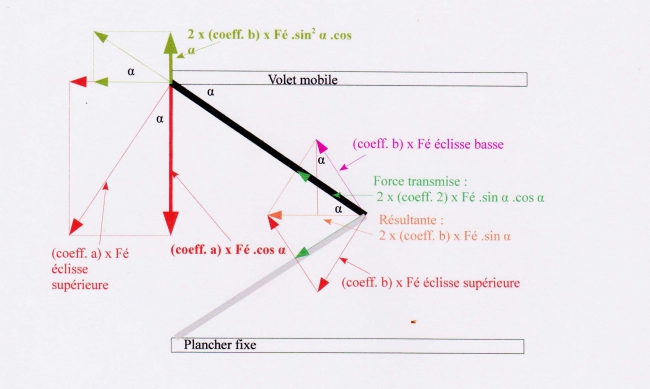
Les forces s’appliquant à l’articulation des deux éclisses (représentées ici en rouge et rose) ont une résultante (représentée en orange) dans l’axe de la pliure qui peut être décomposée en forces (représentées en vert clair) dans les plans des éclisses. Ces forces sont transmises à l’extrémité de l’éclisse articulée avec le volet (ou avec le support) - en supposant l’éclisse rigide - et sont alors représentées en vert foncé.
Les forces s’appliquant à l’articulation avec le volet peuvent à leur tour être décomposées en forces efficaces – les composantes perpendiculaires au volet - et les composantes tangentielles qui n’ont pas d’effet dans notre étude.
Les forces aboutissant au support (plancher fixe) n'ont pas d'effet.
Puisque nous passerons par les couples engendrés par les différentes forces en jeu, nous ne retiendrons que les composantes perpendiculaires :
1/ des forces tendant à refermer le volet à l’articulation des éclisses avec le volet (en rouge), qui sont de : (coefficient approprié) x Fé x cos α [α est l’angle que forme l’éclisse avec le volet mobile ou avec le support].
2/ et de la poussée transmise par la combinaison des deux éclisses (en vert foncé), qui s’oppose à la fermeture, qui est de : (coefficient approprié) x 2 x Fé x sin2 α .cos α
Le signe “-” est attribué aux forces tendant à refermer le volet (en rouge), le signe “+” à celles qui tendent à l'ouvrir (en vert foncé).( Le “+” est le sens des aiguilles d'une montre pour mon croquis)
Pour la partie d'éclisse A
La force de fermeture « utile » due aux éclisses haute et basse est donc de :
Féu (A) = ( - 0,586 . cos α + 2 x 0,414 . sin2 α . cos α) x surface A x Pression
Pour les parties d'éclisses B
La force de fermeture « utile » due aux éclisses haute et basse est de :
Féu (B) = ( - 0,66 . cos α + 2 x 0,33 . sin2 α . cos α) x surface B x Pression
Les points virtuels d’application de ces forces (bras de levier) se situent :
-
à l’extrémité du volet pour les forces concernant l'éclisse A
-
au 2/3 de la longueur du volet pour les forces concernant les éclisses longitudinales B
Soit, pour ma réalisation, respectivement à une distance de 36,5 cm et 24,3 cm de l'articulation.
Couples engendrés
Ces forces ainsi définies agissent selon la distance de leur point d’application avec le point d’articulation du volet (bras de levier).
Couple dû à la pression sur les éclisses :
Féu (A) x Longueur volet + Féu (B) x Longueur volet x 2/3
= ( - 0,586 . cos α + 2 x 0,414 . sin2 α . cos α) x surface A x Longueur volet x Pression
+ ( - 0,66 . cos α + 2 x 0,33 . sin2 α . cos α) x surface B x Longueur volet x 2/3 x Pression.
Couple résultant de l'interaction avec le volet :
= surface volet x longueur volet / 2 x Pression
+ ( - 0,586 . cos α + 2 x 0,414 . sin2 α . cos α) x surface A x Longueur volet x Pression
+ ( - 0,66 . cos α + 2 x 0,33 . sin2 α . cos α) x surface B x Longueur volet x 2/3 x Pression.
Dans l'exemple de ma réalisation, on peut avec cette formule calculer le couple généré par une pression donnée, en fonction du débattement du volet de la réserve. (Voir en annexe la relation entre α , l'angle que font les éclisses avec le volet mobile, et ce débattement)
Ressort
A pression constante, le couple résultant varie donc en fonction de la position du volet (débattement d), c'est à dire de α , l’angle que font les éclisses avec le volet mobile ou le support, lequel est variable de environ 45° (d maxi) à 0° (d mini, volume réserve mini)
Il doit être compensé par un couple opposé dont le bras de levier est la distance entre le point d’articulation du volet et le point de tire (ou de pression) du ressort (soit 36 cm dans ma réalisation). Si ce couple opposé est à tout instant égal au couple calculé plus haut, la pression interne restera constante pendant toute la phase d’utilisation de la réserve.
Vérifions la validité du calcul par des essais :
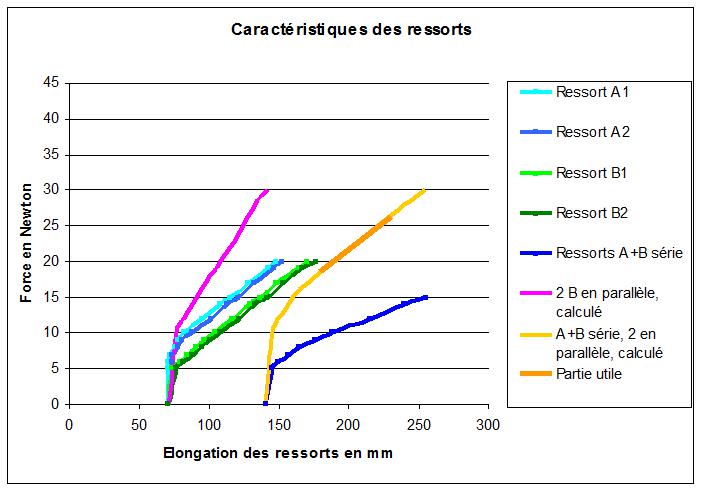
Il se trouve que, pour ces essais, je disposais de quatre ressorts de traction prélevés sur une petite lampe d’architecte. Je les ai étalonnés (réalisation d’un diagramme poids / longueur).
Voilà le résultat ci dessous. Il se trouve (chance!) qu'une des combinaisons possibles de ces ressorts correspond presque exactement au couple calculé.
Avec l’exemple ci dessus, traçons les couples obtenus avec des ressorts d'essai A et B, montés ou pas en série, un ensemble de chaque côté du soufflet, avec les allonges nécessaires pour caler les valeurs. (voir photo):
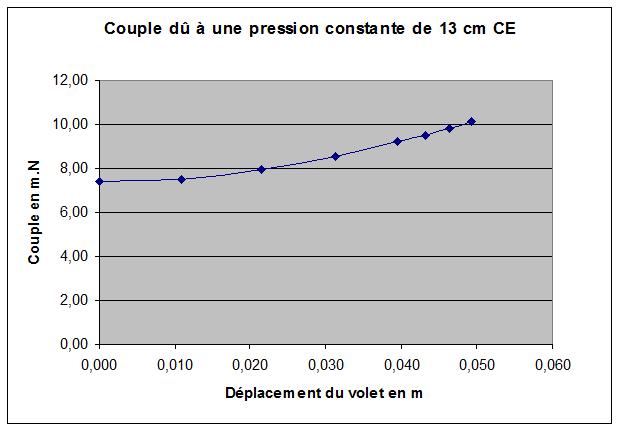
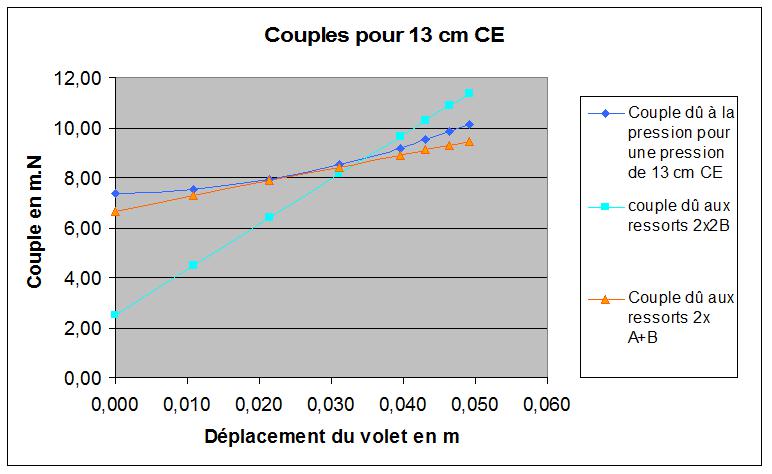
Pour une pression souhaitée de P = 13 cm CE ( = 0,13 N/cm2 )
On voit que la combinaison de ressorts A + B série parallèle (droite orange) colle d'assez près le couple calculé (courbe bleu foncé), alors que la combinaison de ressorts B en parallèle (droite bleu clair) n'a pas la même pente.
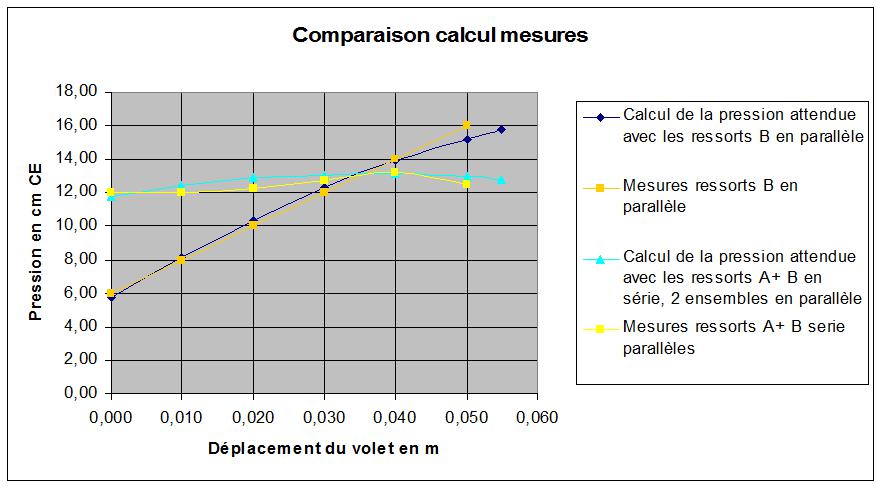
Des essais dans ces deux configurations donnent les mesures suivantes, comparées à la pression attendue par le calcul.
Au vu de l'allure des courbes, on peut considérer que les calculs sont validés. Si les valeurs absolues de pression calculées ne sont pas précises à mieux que le cm d'eau, des essais sous Excel montrent que le calcul est très sensible aux paramètres de base : quelques mm sur les largeurs des éclisses ou du volet changent rapidement le résultat.
L'important à mon sens , et le but recherché, est la stabilité de la pression qui est rendue indépendante dans une large mesure de la position du volet de la réserve.
C'est bien sûr - on le voit dans cet essai de validation – directement lié à la raideur du ressort, qu'il convient d'adapter aux caractéristiques de la réserve.
Cas d'une réserve en dépression
Ce qui précède concerne et est validé pour une réserve à soufflets en pression. Pour une réserve en dépression, on peut faire le même calcul. Il convient de se reporter aux calculs ci-avant, et d'appliquer la même convention :
Le signe “-” est attribué aux forces tendant à refermer le volet (en rouge), le signe “+” à celles qui tendent à l'ouvrir (en vert foncé).( Le “+” est le sens des aiguilles d'une montre pour mon croquis)
Les formules restent identiques:
Couple dû à la pression sur les éclisses :
Féu (A) x Longueur volet + Féu (B) x Longueur volet x 2/3
= ( - 0,586 . cos α + 2 x 0,414 . sin2 α . cos α) x surface A x Longueur volet x Pression
+ ( - 0,66 . cos α + 2 x 0,33 . sin2 α . cos α) x surface B x Longueur volet x 2/3 x Pression.
Couple résultant de l'interaction avec le volet :
= surface volet x longueur volet / 2 x Pression
+ ( - 0,586 . cos α + 2 x 0,414 . sin2 α . cos α) x surface A x Longueur volet x Pression
+ ( - 0,66 . cos α + 2 x 0,33 . sin2 α . cos α) x surface B x Longueur volet x 2/3 x Pression.
Mais la pression étant cette fois négative, le résultat l'est aussi
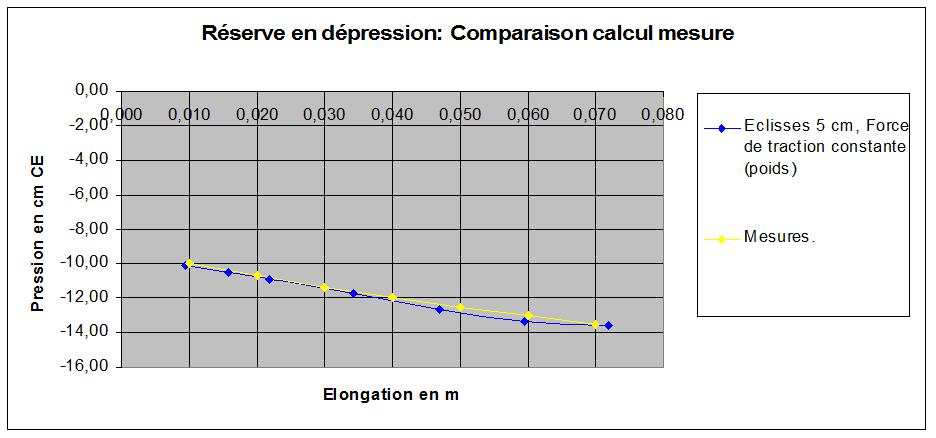
Ces calculs, réalises sur ma construction en cours d'un orgue à anches dont la réserve est en dépression donnent les résultats suivants, comparés avec les mesures effectuées:
Nous savons donc calculer la pression prévisible d'une réserve à soufflet dans les deux configurations: pression et dépression.
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 21 autres membres